

16個の点が次のように整列しています。この点のうち6個の点を通る円はいくつ描けるでしょうか?

こういうことです。
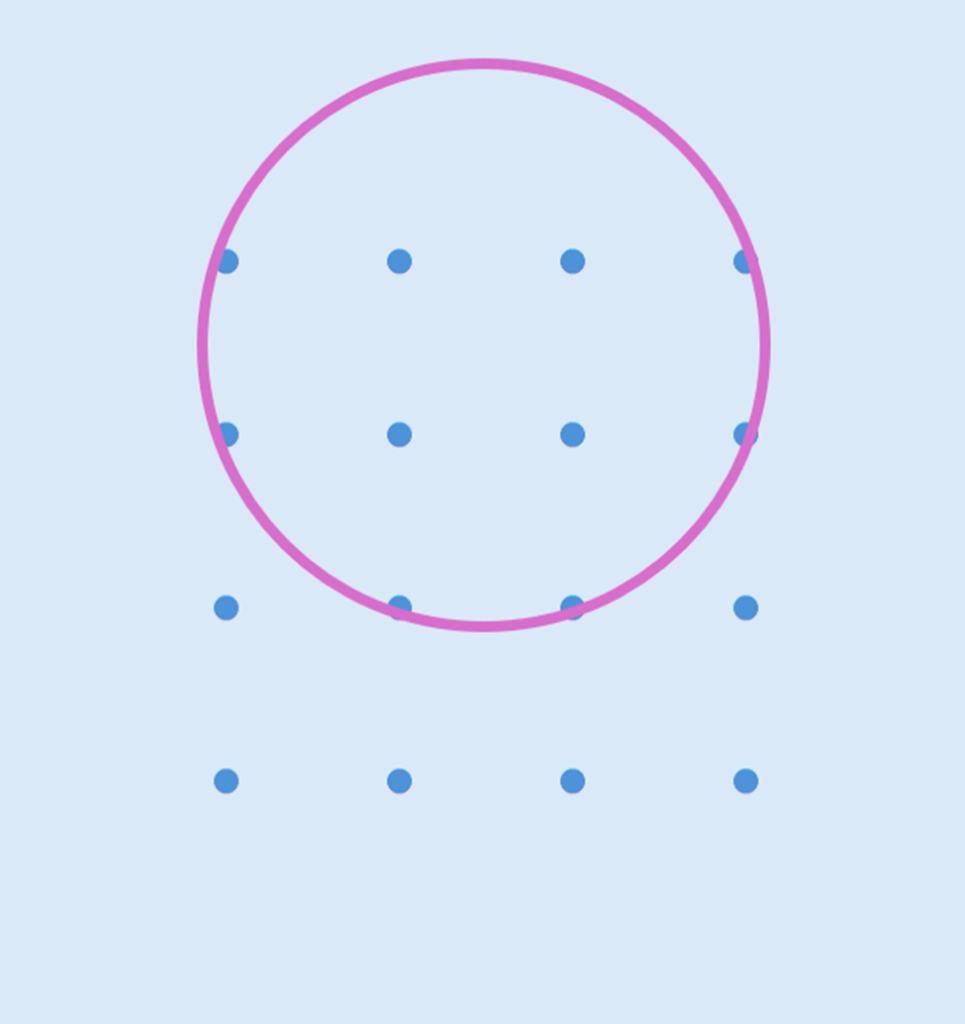
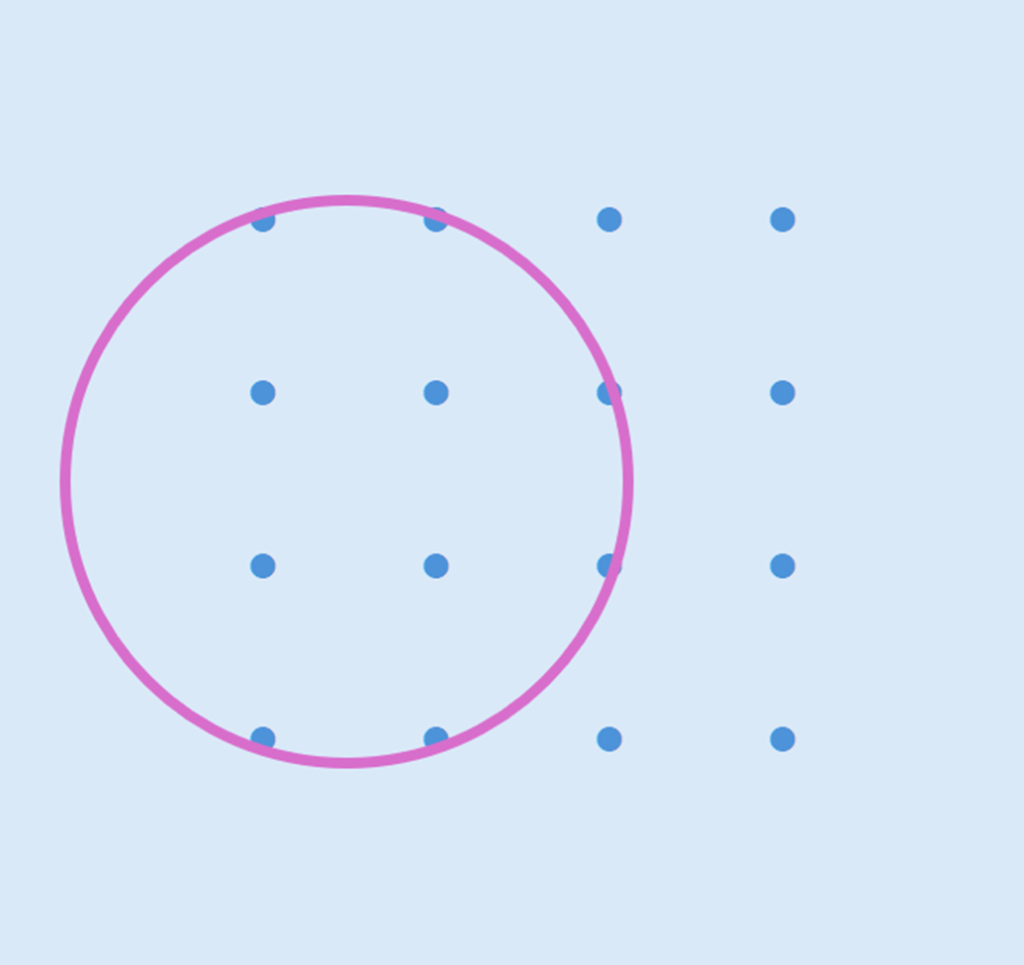
これをVBAで解決してみます。
① ExcelのSheet1のセルの幅を調整します。高さも幅も20ピクセルにします。
② セルP16:AD30に線を引きます。
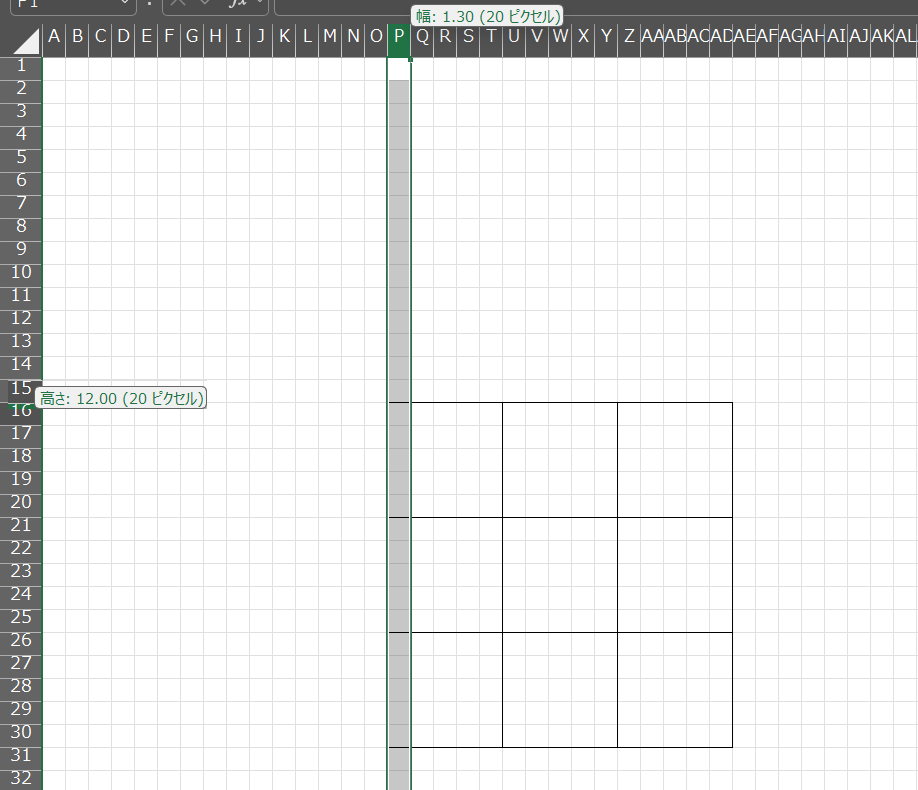
③ ②で用意した正方形4つの交点を以下のように見立てます。
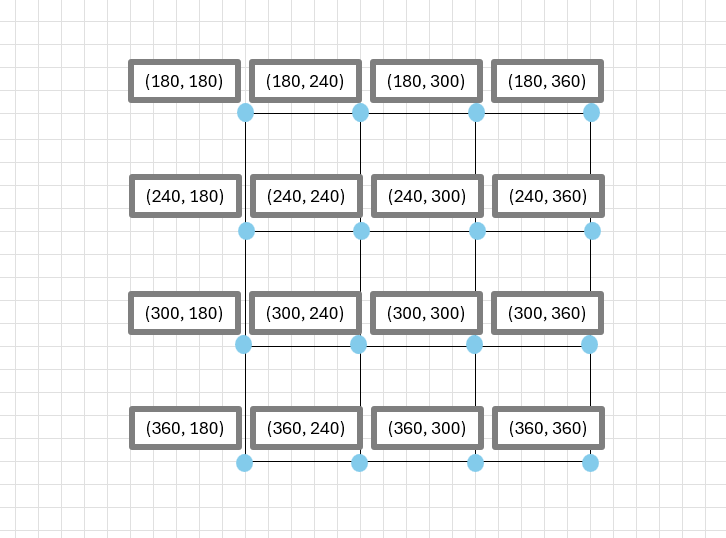
④ 次のプログラムをModule1に記載します。
Option Explicit
' 円が点を通る数
Public Const POINT_CNT As Long = 6
Public Sub makeRingsInSquare()
' タイトル
Const TITLE As String = "make Rings In Square"
' 単純なループカウンタ
Dim lp1 As Long, lp2 As Long, lp3 As Long
' パズルの解析を始めるか問い合わせる。
Dim ret
ret = MsgBox( _
"パズルの解析を始めますか?" _
, vbYesNo + vbQuestion _
, TITLE _
)
' [No]の場合は処理を継続しない。
If ret = vbNo Then
Exit Sub
End If
' 点を表す座標配列を作成する。
Dim pointArray() As Integer
pointArray = makePointArray
' 描くことができた円の数をカウントするための変数
Dim ringsCnt As Long
ringsCnt = 0
' 作業用連想配列
Dim hs As Object
' +++++++++++++++++++++++++++++++++++++
' 正方形の中を移動しながら、
' その点を中心に等距離にある点を探す。
' +++++++++++++++++++++++++++++++++++++
For lp1 = 180 To 360
For lp2 = 180 To 360
' 作業用連想配列の初期化を行う。
Set hs = CreateObject("Scripting.Dictionary")
' 点の存在する座標との距離を一つずつ調べる。
For lp3 = 1 To UBound(pointArray, 1)
' 距離を格納する変数
Dim length As Double
length = Sqr((pointArray(lp3, 1) - lp1) ^ 2 _
+ (pointArray(lp3, 2) - lp2) ^ 2)
' 既に等距離の点を発見済みかどうか判別する。
If hs.Exists(length) Then
' 発見済みの場合には連想配列を更新する。
Dim c As Long
c = hs.Item(length) + 1
hs.Remove (length)
hs.Add length, c
Else
' 初めて登場する距離は、連想配列に登録する。
hs.Add length, 1
End If
Next lp3
' 作成した連想配列のKeyを通常の配列に変換する。
Dim r
r = hs.Keys
' 等距離に存在した点がPOINT_CNT個であれば、円を描く。
For lp3 = LBound(r) To UBound(r)
If hs.Item(r(lp3)) = POINT_CNT Then
ActiveSheet.Shapes.AddShape _
(Type:=msoShapeOval _
, Left:=CDbl(lp1 - r(lp3)) _
, Top:=CDbl(lp2 - r(lp3)) _
, Width:=CDbl(2 * r(lp3)) _
, Height:=CDbl(2 * r(lp3)) _
).Select
Selection.ShapeRange.Fill.Visible = msoFalse
' 描いた円の数をカウントアップする。
ringsCnt = ringsCnt + 1
Application.Wait Now + TimeValue("00:00:01")
End If
Next lp3
' 作業用連想配列を解放する。
Set hs = Nothing
Next lp2
Next lp1
' 処理の終了を表示する。
MsgBox ringsCnt & "個の円が描けました。" _
, vbInformation _
, TITLE
' メモリを解放する。
Erase pointArray
End Sub
Private Function makePointArray() As Integer()
' 点を表す座標配列を作成する。
Dim ret(16, 2) As Integer
' 上段の点の座標を確定する。
ret(1, 1) = 180
ret(1, 2) = 180
ret(2, 1) = 240
ret(2, 2) = 180
ret(3, 1) = 300
ret(3, 2) = 180
ret(4, 1) = 360
ret(4, 2) = 180
' 二段目の点の座標を確定する。
ret(5, 1) = 180
ret(5, 2) = 240
ret(6, 1) = 240
ret(6, 2) = 240
ret(7, 1) = 300
ret(7, 2) = 240
ret(8, 1) = 360
ret(8, 2) = 240
' 三段目の点の座標を確定する。
ret(9, 1) = 180
ret(9, 2) = 300
ret(10, 1) = 240
ret(10, 2) = 300
ret(11, 1) = 300
ret(11, 2) = 300
ret(12, 1) = 360
ret(12, 2) = 300
' 下段の点の座標を確定する。
ret(13, 1) = 180
ret(13, 2) = 360
ret(14, 1) = 240
ret(14, 2) = 360
ret(15, 1) = 300
ret(15, 2) = 360
ret(16, 1) = 360
ret(16, 2) = 360
' 作成した座標を呼出し元に返す。
makePointArray = ret
End Function⑤ makeRingsInSquare() を実行します。
結果が得られます。
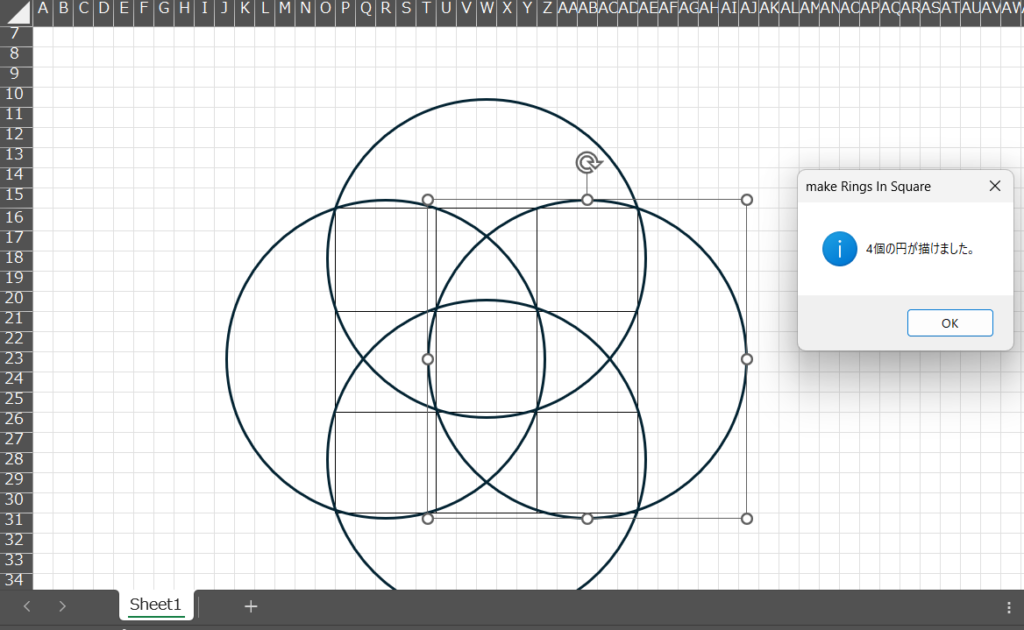
4個でした!




コメントを残す